为何二叉树重要 #

题目 #

为何二叉树那么重要，而不是三叉树、四叉树呢？

分析 #

树是常见的数据结构，如 DOM 树，是一种多叉树。
其中二叉树是一个特别的存在，很重要，很常考。

【注意】本文涉及很多数据结构的知识，所以要“不求甚解” —— 掌握要点和结果，不求细节和过程

如何让性能整体最优？ #

有序结构

• 数组：查找易，增删难
• 链表：增删易，查找难

将两者优点结合起来 —— 二叉搜索树 BST ：查找易，增删易 —— 可使用二分算法

二叉搜索树 BST

• 左节点（包括其后代） <= 根节点
• 右节点（包括其后代） >= 根节点

高级二叉树 #

二叉搜索树 BST ，如果左右不平衡，也无法做到最优。
极端情况下，它就成了链表 —— 这不是我们想要的。

平衡二叉搜索树 BBST ：要求树左右尽量平衡

• 树高度 h 约等于 logn
• 查找、增删，时间复杂度都等于 O(logn)

红黑树：一种自动平衡的二叉树

• 节点分 红/黑 两种颜色，通过颜色转换来维持树的平衡
• 相比于普通平衡二叉树，它维持平衡的效率更高

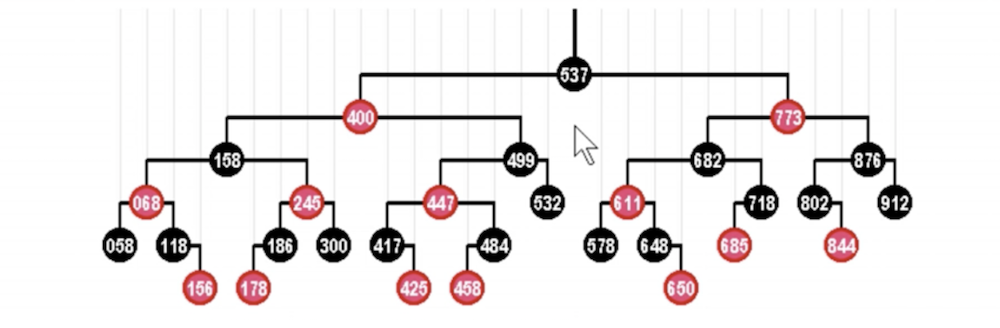
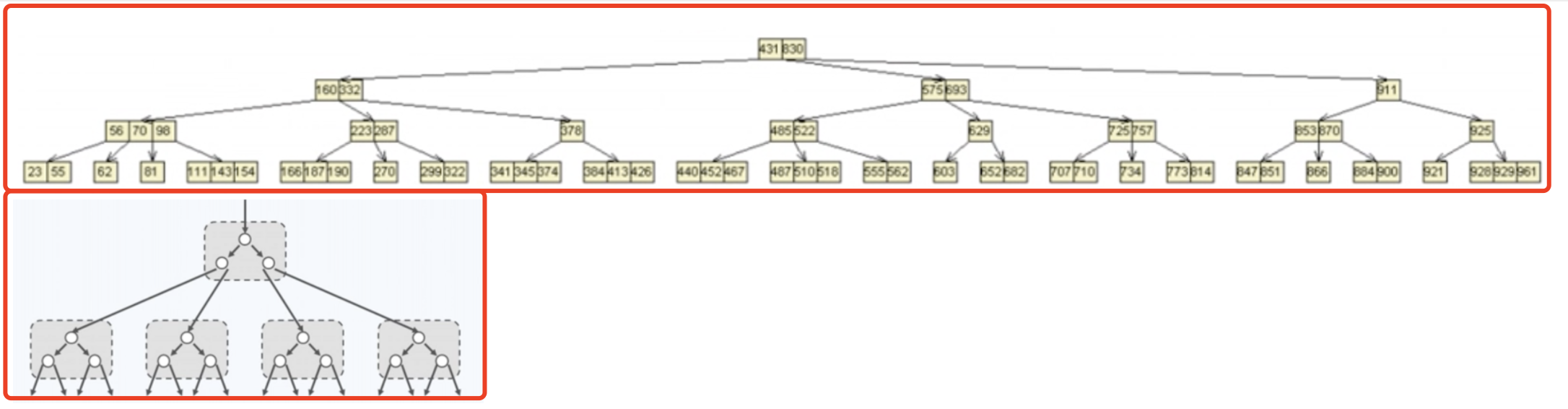
B 树：物理上是多叉树，但逻辑上是一个 BST 。用于高效 I/O ，如关系型数据库就用 B 树来组织数据结构。

堆 #

JS 执行时代码中的变量

• 值类型 - 存储到栈
• 引用类型 - 存储到堆

堆的特点：

• 节点的值，总是不大于（或不小于）其父节点的值
• 完全二叉树

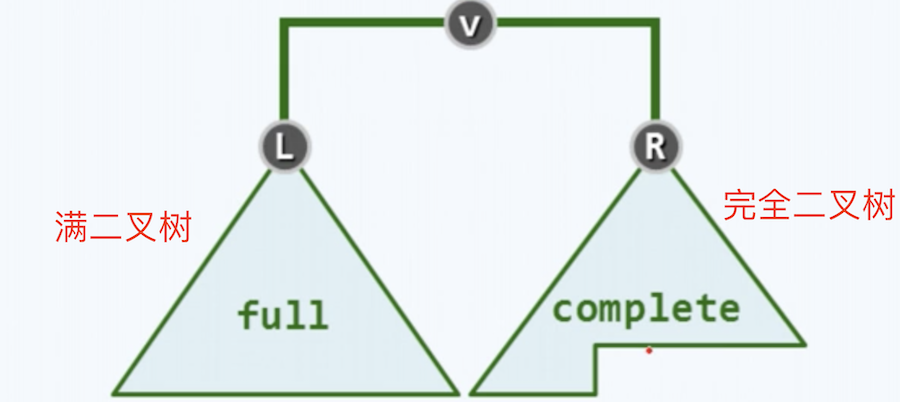
堆，虽然逻辑上是二叉树，但实际上它使用数组来存储的。

// 上图是一个堆（从小到大），可以用数组表示
const heap = [-1, 10, 14, 25, 33, 81, 82, 99] // 忽略 0 节点

// 节点关系
const parentIndex = Math.floor(i / 2)
const leftIndex = 2 * i
const rightIndex = 2 * i + 1

堆的排序规则，没有 BST 那么严格，这就造成了

• 查询比 BST 慢
• 增删比 BST 快，维持平衡也更快
• 但整体复杂度都是 O(logn) 级别，即树的高度

但结合堆的应用场景

• 一般使用内存地址（栈中保存了）来查询，不会直接从根节点搜索
• 堆的物理结构是数组，所以查询复杂度就是 O(1)

总结

• 物理结构是数组（空间更小），逻辑结构是二叉树（操作更快）
• 适用于“堆栈”结构

答案 #

• 二叉树，可以充分利用二分法
• 二叉树可以同时规避数字和链表的缺点
• 引申到 BST BBST 等其他扩展结构

划重点 #

• 二分法的神奇力量
• 各个高级数据结构的存在价值、设计初衷
• 数据结构是基本功能